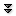When we computed the derivative $dy/dx$ using polar coordinates, we used the expressions $x=f(\theta)\cos\theta$ and $y=f(\theta)\sin\theta$. These two equations completely specify the curve, though the form $r=f(\theta)$ is simpler. The expanded form has the virtue that it can easily be generalized to describe a wider range of curves than can be specified in rectangular or polar coordinates.
Suppose $f(t)$ and $g(t)$ are functions. Then the equations $x=f(t)$ and $y=g(t)$ describe a curve in the plane. In the case of the polar coordinates equations, the variable $t$ is replaced by $\theta$ which has a natural geometric interpretation. But $t$ in general is simply an arbitrary variable, often called in this case a parameter, and this method of specifying a curve is known as parametric equations. One important interpretation of $t$ is time. In this interpretation, the equations $x=f(t)$ and $y=g(t)$ give the position of an object at time $t$.
Example 12.4.1 Describe the path of an object that moves so that its position at time $t$ is given by $x=\cos t$, $\ds y=\cos^2 t$. We see immediately that $\ds y=x^2$, so the path lies on this parabola. The path is not the entire parabola, however, since $x=\cos t$ is always between $-1$ and $1$. It is now easy to see that the object oscillates back and forth on the parabola between the endpoints $(1,1)$ and $(-1,1)$, and is at point $(1,1)$ at time $t=0$. $\square$
It is sometimes quite easy to describe a complicated path in parametric equations when rectangular and polar coordinate expressions are difficult or impossible to devise.
Example 12.4.2 A wheel of radius 1 rolls along a straight line, say the $x$-axis. A point on the rim of the wheel will trace out a curve, called a cycloid. Assume the point starts at the origin; find parametric equations for the curve.
Figure 12.4.1 illustrates the generation of the curve (click on the AP link to see an animation). The wheel is shown at its starting point, and again after it has rolled through about 490 degrees. We take as our parameter $t$ the angle through which the wheel has turned, measured as shown clockwise from the line connecting the center of the wheel to the ground. Because the radius is 1, the center of the wheel has coordinates $(t,1)$. We seek to write the coordinates of the point on the rim as $(t+\Delta x,1+\Delta y)$, where $\Delta x$ and $\Delta y$ are as shown in figure 12.4.2. These values are nearly the sine and cosine of the angle $t$, from the unit circle definition of sine and cosine. However, some care is required because we are measuring $t$ from a nonstandard starting line and in a clockwise direction, as opposed to the usual counterclockwise direction. A bit of thought reveals that $\Delta x=-\sin t$ and $\Delta y=-\cos t$. Thus the parametric equations for the cycloid are $x=t-\sin t$, $y=1-\cos t$. $\square$
Exercises 12.4
You can plot parametric functions with Sage.
Ex 12.4.1 What curve is described by $\ds x=t^2$, $\ds y=t^4$? If $t$ is interpreted as time, describe how the object moves on the curve.
Ex 12.4.2 What curve is described by $x=3\cos t$, $y=3\sin t$? If $t$ is interpreted as time, describe how the object moves on the curve.
Ex 12.4.3 What curve is described by $x=3\cos t$, $y=2\sin t$? If $t$ is interpreted as time, describe how the object moves on the curve.
Ex 12.4.4 What curve is described by $x=3\sin t$, $y=3\cos t$? If $t$ is interpreted as time, describe how the object moves on the curve.
Ex 12.4.5 Sketch the curve described by $\ds x=t^3-t$, $\ds y=t^2$. If $t$ is interpreted as time, describe how the object moves on the curve.
Ex 12.4.6 A wheel of radius 1 rolls along a straight line, say the $x$-axis. A point $P$ is located halfway between the center of the wheel and the rim; assume $P$ starts at the point $(0,1/2)$. As the wheel rolls, $P$ traces a curve; find parametric equations for the curve. (answer)
Ex 12.4.7 A wheel of radius 1 rolls around the outside of a circle of radius 3. A point $P$ on the rim of the wheel traces out a curve called a hypercycloid, as indicated in figure 12.4.3. Assuming $P$ starts at the point $(3,0)$, find parametric equations for the curve. (answer)
Ex 12.4.8 A wheel of radius 1 rolls around the inside of a circle of radius 3. A point $P$ on the rim of the wheel traces out a curve called a hypocycloid, as indicated in figure 12.4.3. Assuming $P$ starts at the point $(3,0)$, find parametric equations for the curve. (answer)
Ex 12.4.9 An involute of a circle is formed as follows: Imagine that a long (that is, infinite) string is wound tightly around a circle, and that you grasp the end of the string and begin to unwind it, keeping the string taut. The end of the string traces out the involute. Find parametric equations for this curve, using a circle of radius 1, and assuming that the string unwinds counter-clockwise and the end of the string is initially at $(1,0)$. Figure 12.4.4 shows part of the curve; the dotted lines represent the string at a few different times. (answer)