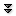The average of some finite set of values is a familiar concept. If, for example, the class scores on a quiz are 10, 9, 10, 8, 7, 5, 7, 6, 3, 2, 7, 8, then the average score is the sum of these numbers divided by the size of the class: $$ \hbox{average score} = {10+ 9+ 10+ 8+ 7+ 5+ 7+ 6+ 3+ 2+ 7+ 8\over 12}={82\over 12}\approx 6.83. $$ Suppose that between $t=0$ and $t=1$ the speed of an object is $\sin(\pi t)$. What is the average speed of the object over that time? We know one way to make sense of this: average speed is distance traveled divided by elapsed time. The distance traveled is $\ds\int_0^1 \sin(\pi t)\,dt=2/\pi\approx 0.64$, and elapsed time is $1$, so the average speed is $2/\pi$. This appears to have nothing to do with the simple idea of average, as in the case of the quiz scores. We might also want to compute an average not tied to speed; for example, what is the average height of the curve $\sin(\pi t)$ over the interval $[0,1]$? Is it the same as the average speed? More generally, can we make sense of the average of $f(x)$ over an interval $[a,b]$?

To make sense of "average'' in this more general context, we fall back on the idea of approximation. What is the average of $\sin(\pi t)$ over the interval $[0,1]$? We might reasonably approximate this by choosing some $t$ values in the interval $[0,1]$, add up the corresponding values of $\sin(\pi t)$, and then divide by the number of values. If we divide $[0,1]$ into $10$ equal subintervals, we get $$ {1\over 10}\sum_{i=0}^9 \sin(\pi i/10)\approx {1\over 10}6.3=0.63. $$ If we compute more values of the function at more values of $t$, the average of these values should be closer to the "real'' average. If we take the average of $n$ values for evenly spaced values of $t$, we get: $${1\over n}\sum_{i=0}^{n-1} \sin(\pi i/n).$$ Here the individual values of $t$ are $\ds t_i=i/n$, so rewriting slightly we have $${1\over n}\sum_{i=0}^{n-1} \sin(\pi t_i).$$ This is almost the sort of sum that we know turns into an integral; what's apparently missing is $\Delta t$—but in fact, $\Delta t=1/n$, the length of each subinterval. So rewriting again: $$ \sum_{i=0}^{n-1} \sin(\pi t_i){1\over n}= \sum_{i=0}^{n-1} \sin(\pi t_i)\Delta t. $$ Now this has exactly the right form, so that in the limit we get $$ \hbox{average} = \int_0^1 \sin(\pi t)\,dt= \left.-{\cos(\pi t)\over\pi}\right|_0^1= -{\cos(\pi)\over \pi}+{\cos(0)\over\pi}={2\over\pi}\approx 0.64. $$ Of course, this is exactly what we computed before, but we didn't need to rely on a particular interpretation of the function. If we interpret $\sin(\pi t)$ as the height of the function, we interpret the result as the average height of $\sin(\pi t)$ over $[0,1]$. It's not entirely obvious from this one simple example how to compute such an average in general. Let's look at a somewhat more complicated case. Suppose that the function is $\ds 16 t^2+5$. What is the average between $t=1$ and $t=3$? Again we set up an approximation to the average: $${1\over n}\sum_{i=0}^{n-1} 16t_i^2+5,$$ where the values $\ds t_i$ are evenly spaced between 1 and 3. Once again we are "missing'' $\Delta t$, and this time $1/n$ is not the correct value. What is $\Delta t$ in general? It is the length of a subinterval; in this case we take the interval $[1,3]$ and divide it into $n$ subintervals, so each has length $(3-1)/n=2/n=\Delta t$. Now with the usual "multiply and divide by the same thing'' trick we can rewrite the sum: $$ {1\over n}\sum_{i=0}^{n-1} 16t_i^2+5= {1\over 3-1}\sum_{i=0}^{n-1} (16t_i^2+5){3-1\over n}= {1\over 2}\sum_{i=0}^{n-1} (16t_i^2+5){2\over n}= {1\over 2}\sum_{i=0}^{n-1} (16t_i^2+5)\Delta t. $$ In the limit this becomes $${1\over 2}\int_1^3 16t^2+5\,dt={1\over 2}{446\over 3}={223\over 3}.$$ Does this seem reasonable? Let's picture it: in figure 8.4.1 is the function $16t_i^2+5$ together with the horizontal line $y=223/3\approx 74.3$. Certainly the height of the horizontal line looks at least plausible for the average height of the curve.