We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''.
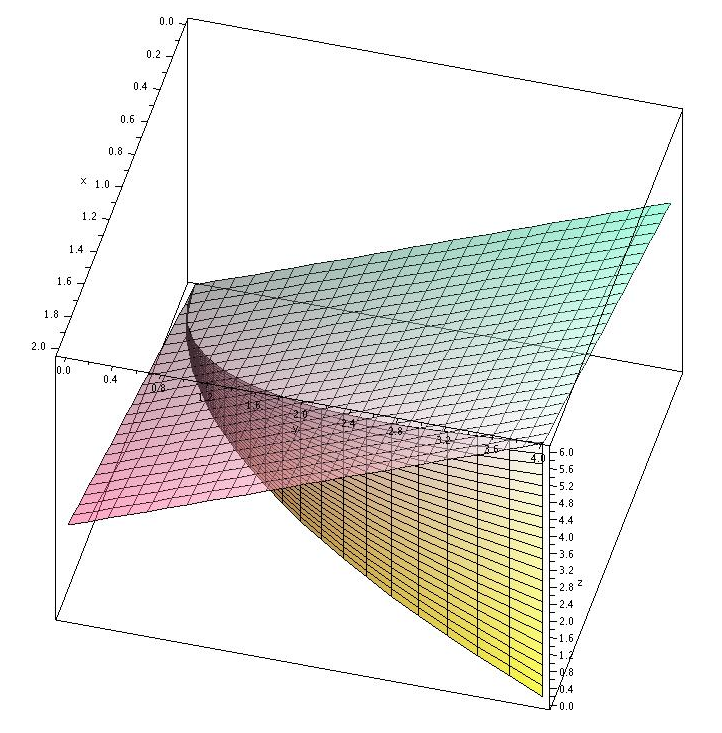
As with other integrals, a geometric example may be easiest to understand. Consider the function $f=x+y$ and the parabola $y=x^2$ in the $x$-$y$ plane, for $0\le x\le 2$. Imagine that we extend the parabola up to the surface $f$, to form a curved wall or curtain, as in figure 16.2.1. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come.
|
|
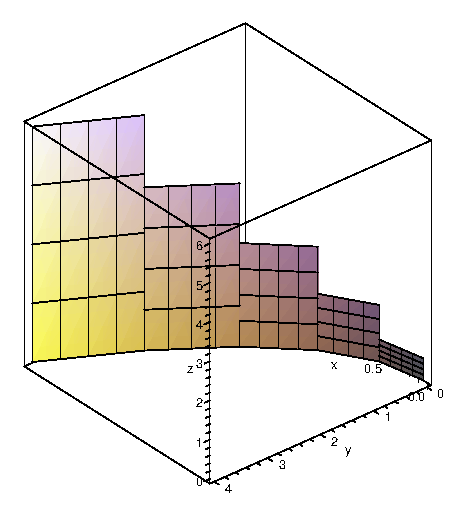
As usual, we start by thinking about how to approximate the area. We pick some points along the part of the parabola we're interested in, and connect adjacent points by straight lines; when the points are close together, the length of each line segment will be close to the length along the parabola. Using each line segment as the base of a rectangle, we choose the height to be the height of the surface $f$ above the line segment. If we add up the areas of these rectangles, we get an approximation to the desired area, and in the limit this sum turns into an integral.
Typically the curve is in vector form, or can easily be put in vector form; in this example we have ${\bf r}(t)=\langle t,t^2\rangle$. Then as we have seen in section 13.3 on arc length, the length of one of the straight line segments in the approximation is approximately $ds=|{\bf r}'|\,dt=\sqrt{1+4t^2}\,dt$, so the integral is $$\int_0^2 f(t,t^2)\sqrt{1+4t^2}\,dt =\int_0^2 (t+t^2)\sqrt{1+4t^2}\,dt= {167\over48}\sqrt{17}-{1\over12}-{1\over64}\ln(4+\sqrt{17}). $$ This integral of a function along a curve $C$ is often written in abbreviated form as $$\int_C f(x,y)\,ds.$$
Example 16.2.1 Compute $\ds\int_C ye^x\,ds$ where $C$ is the line segment from $(1,2)$ to $(4,7)$.
We write the line segment as a vector function: ${\bf r}=\langle 1,2\rangle + t\langle 3,5\rangle$, $0\le t\le 1$, or in parametric form $x=1+3t$, $y=2+5t$. Then $$\int_C ye^x\,ds = \int_0^1 (2+5t)e^{1+3t}\sqrt{3^2+5^2}\,dt ={16\over 9}\sqrt{34}e^4-{1\over9}\sqrt{34}\,e. $$ $\square$
All of these ideas extend to three dimensions in the obvious way.
Example 16.2.2 Compute $\ds\int_C x^2 z \,ds$ where $C$ is the line segment from $(0,6,-1)$ to $(4,1,5)$.
We write the line segment as a vector function: ${\bf r}=\langle 0,6,-1\rangle + t\langle 4,-5,6\rangle$, $0\le t\le 1$, or in parametric form $x=4t$, $y=6-5t$, $z=-1+6t$. Then $$\int_C x^2 z\,ds = \int_0^1 (4t)^2 (-1+6t)\sqrt{16+25+36}\,dt =16\sqrt{77}\int_0^1 -t^2+6t^3\,dt={56\over3}\sqrt{77}. $$ $\square$
Now we turn to a perhaps more interesting example. Recall that in the simplest case, the work done by a force on an object is equal to the magnitude of the force times the distance the object moves; this assumes that the force is constant and in the direction of motion. We have already dealt with examples in which the force is not constant; now we are prepared to examine what happens when the force is not parallel to the direction of motion.
We have already examined the idea of components of force, in example 12.3.4: the component of a force $\bf F$ in the direction of a vector $\bf v$ is $${{\bf F}\cdot {\bf v}\over|{\bf v}|^2}{\bf v},$$ the projection of $\bf F$ onto $\bf v$. The magnitude of the force in the direction of $\bf v$ is the scalar projection of $\bf F$ onto $\bf v$: $${{\bf F}\cdot {\bf v}\over|{\bf v}|}.$$ If an object moves subject to this (constant) force, in the direction of $\bf v$, over a distance equal to the length of $\bf v$, the work done is $${{\bf F}\cdot {\bf v}\over|{\bf v}|}|{\bf v}|={\bf F}\cdot {\bf v}.$$ Thus, work in the vector setting is still "force times distance'', except that "times'' means "dot product''.
If the force varies from point to point, it is represented by a vector field $\bf F$; the displacement vector $\bf v$ may also change, as an object may follow a curving path in two or three dimensions. Suppose that the path of an object is given by a vector function ${\bf r}(t)$; at any point along the path, the (small) tangent vector ${\bf r}'\,\Delta t$ gives an approximation to its motion over a short time $\Delta t$, so the work done during that time is approximately ${\bf F}\cdot{\bf r}'\,\Delta t$; the total work over some time period is then $$\int_{t_0}^{t_1} {\bf F}\cdot{\bf r}'\,dt.$$ It is useful to rewrite this in various ways at different times. We start with $$\int_{t_0}^{t_1} {\bf F}\cdot{\bf r}'\,dt=\int_C {\bf F}\cdot\,d{\bf r},$$ abbreviating ${\bf r}'\,dt$ by $d{\bf r}$. Or we can write $$\int_{t_0}^{t_1} {\bf F}\cdot{\bf r}'\,dt= \int_{t_0}^{t_1} {\bf F}\cdot{{\bf r}'\over|{\bf r}'|}|{\bf r}'|\,dt= \int_{t_0}^{t_1} {\bf F}\cdot{\bf T}\,|{\bf r}'|\,dt= \int_{C} {\bf F}\cdot{\bf T}\,ds,$$ using the unit tangent vector $\bf T$, abbreviating $|{\bf r}'|\,dt$ as $ds$, and indicating the path of the object by $C$. In other words, work is computed using a particular line integral of the form we have considered. Alternately, we sometimes write $$\eqalign{ \int_C {\bf F}\cdot{\bf r}'\,dt&= \int_C \langle f,g,h\rangle\cdot\langle x',y',z'\rangle\,dt= \int_C \left(f{dx\over dt}+g{dy\over dt}+h{dz\over dt}\right)\,dt\cr &= \int_C f\,dx+g\,dy+h\,dz= \int_C f\,dx+\int_C g\,dy+\int_C h\,dz,\cr}$$ and similarly for two dimensions, leaving out references to $z$.
Example 16.2.3 Suppose an object moves from $(-1,1)$ to $(2,4)$ along the path ${\bf r}(t)=\langle t,t^2\rangle$, subject to the force ${\bf F}=\langle x\sin y,y\rangle$. Find the work done.
We can write the force in terms of $t$ as $\langle t\sin(t^2),t^2\rangle$, and compute ${\bf r}'(t)=\langle 1,2t\rangle$, and then the work is $$\int_{-1}^2 \langle t\sin(t^2),t^2\rangle\cdot\langle 1,2t\rangle\,dt = \int_{-1}^2 t\sin(t^2) + 2t^3\,dt={15\over2}+{\cos(1)-\cos(4)\over2}. $$
Alternately, we might write $$\int_C x\sin y\,dx+\int_C y\,dy= \int_{-1}^2 x\sin(x^2)\,dx + \int_1^4 y\,dy= -{\cos(4)\over 2}+{\cos(1)\over 2}+{16\over2}-{1\over2}$$ getting the same answer. $\square$
Exercises 16.2
Here is a Sage cell if you'd like to use it.
Ex 16.2.1 Compute $\ds\int_C xy^2\,ds$ along the line segment from $(1,2,0)$ to $(2,1,3)$. (answer)
Ex 16.2.2 Compute $\ds\int_C \sin x\,ds$ along the line segment from $(-1,2,1)$ to $(1,2,5)$. (answer)
Ex 16.2.3 Compute $\ds\int_C z\cos(xy)\,ds$ along the line segment from $(1,0,1)$ to $(2,2,3)$. (answer)
Ex 16.2.4 Compute $\ds\int_C \sin x\,dx+\cos y\,dy$ along the top half of the unit circle, from $(1,0)$ to $(-1,0)$. (answer)
Ex 16.2.5 Compute $\ds\int_C xe^y\,dx+x^2y\,dy$ along the line segment $y=3$, $0\le x\le 2$. (answer)
Ex 16.2.6 Compute $\ds\int_C xe^y\,dx+x^2y\,dy$ along the line segment $x=4$, $0\le y\le 4$. (answer)
Ex 16.2.7 Compute $\ds\int_C xe^y\,dx+x^2y\,dy$ along the curve $x=3t$, $y=t^2$, $0\le t\le1$. (answer)
Ex 16.2.8 Compute $\ds\int_C xe^y\,dx+x^2y\,dy$ along the curve $\langle e^t,e^t\rangle$, $-1\le t\le1$. (answer)
Ex 16.2.9 Compute $\ds\int_C \langle \cos x,\sin y\rangle\cdot d{\bf r}$ along the curve $\langle t,t\rangle$, $0\le t\le1$. (answer)
Ex 16.2.10 Compute $\ds\int_C \langle 1/xy,1/(x+y)\rangle\cdot d{\bf r}$ along the path from $(1,1)$ to $(3,1)$ to $(3,6)$ using straight line segments. (answer)
Ex 16.2.11 Compute $\ds\int_C \langle 1/xy,1/(x+y)\rangle\cdot d{\bf r}$ along the curve $\langle 2t,5t\rangle$, $1\le t\le 4$. (answer)
Ex 16.2.12 Compute $\ds\int_C \langle 1/xy,1/(x+y)\rangle\cdot d{\bf r}$ along the curve $\langle t,t^2\rangle$, $1\le t\le 4$. (answer)
Ex 16.2.13 Compute $\ds\int_C yz\,dx+xz\,dy+xy\,dz$ along the curve $\langle t,t^2,t^3\rangle$, $0\le t\le1$. (answer)
Ex 16.2.14 An object moves from $(1,1)$ to $(4,8)$ along the path ${\bf r}(t)=\langle t^2,t^3\rangle$, subject to the force ${\bf F}=\langle x^2,\sin y\rangle$. Find the work done. (answer)
Ex 16.2.15 An object moves along the line segment from $(1,1)$ to $(2,5)$, subject to the force ${\bf F}=\langle x/(x^2+y^2),y/(x^2+y^2)\rangle$. Find the work done. (answer)
Ex 16.2.16 An object moves along the parabola ${\bf r}(t)=\langle t,t^2\rangle$, $0\le t\le1$, subject to the force ${\bf F}=\langle 1/(y+1),-1/(x+1)\rangle$. Find the work done. (answer)
Ex 16.2.17 An object moves along the line segment from $(0,0,0)$ to $(3,6,10)$, subject to the force ${\bf F}=\langle x^2,y^2,z^2\rangle$. Find the work done. (answer)
Ex 16.2.18 An object moves along the curve ${\bf r}(t)=\langle \sqrt{t},1/\sqrt{t},t\rangle$ $1\le t\le4$, subject to the force ${\bf F}=\langle y,z,x\rangle$. Find the work done. (answer)
Ex 16.2.19 An object moves from $(1,1,1)$ to $(2,4,8)$ along the path ${\bf r}(t)=\langle t,t^2,t^3\rangle$, subject to the force ${\bf F}=\langle \sin x,\sin y,\sin z\rangle$. Find the work done. (answer)
Ex 16.2.20 An object moves from $(1,0,0)$ to $(-1,0,\pi)$ along the path ${\bf r}(t)=\langle \cos t,\sin t, t\rangle$, subject to the force ${\bf F}=\langle y^2,y^2,xz\rangle$. Find the work done. (answer)
Ex 16.2.21 Give an example of a non-trivial force field ${\bf F}$ and non-trivial path ${\bf r}(t)$ for which the total work done moving along the path is zero.
