Suppose a surface given by $f(x,y)$ has a local maximum at $(x_0,y_0,z_0)$; geometrically, this point on the surface looks like the top of a hill. If we look at the cross-section in the plane $y=y_0$, we will see a local maximum on the curve at $(x_0,z_0)$, and we know from single-variable calculus that ${\partial z\over\partial x}=0$ at this point. Likewise, in the plane $x=x_0$, ${\partial z\over\partial y}=0$. So if there is a local maximum at $(x_0,y_0,z_0)$, both partial derivatives at the point must be zero, and likewise for a local minimum. Thus, to find local maximum and minimum points, we need only consider those points at which both partial derivatives are 0. As in the single-variable case, it is possible for the derivatives to be 0 at a point that is neither a maximum or a minimum, so we need to test these points further.
You will recall that in the single variable case, we examined three methods to identify maximum and minimum points; the most useful is the second derivative test, though it does not always work. For functions of two variables there is also a second derivative test; again it is by far the most useful test, though it doesn't always work.
Theorem 14.7.1 Suppose that the second partial derivatives of $f(x,y)$ are continuous near $(x_0,y_0)$, and $f_x(x_0,y_0)=f_y(x_0,y_0)=0$. We denote by $D$ the discriminant: $$D(x_0,y_0)=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)-f_{xy}(x_0,y_0)^2.$$
| If $D>0$: | ||
| if $f_{xx}(x_0,y_0)< 0$: there is a local maximum at $(x_0,y_0)$; | ||
| if $f_{xx}(x_0,y_0)>0$: there is a local minimum at $(x_0,y_0)$; | ||
| If $D< 0$: | there is neither a maximum nor a minimum at $(x_0,y_0)$; | |
| If $D=0$: | the test fails. |
Example 14.7.2 Verify that $f(x,y)=x^2+y^2$ has a minimum at $(0,0)$.
First, we compute all the needed derivatives: $$f_x=2x \qquad f_y=2y \qquad f_{xx}=2 \qquad f_{yy}=2 \qquad f_{xy}=0.$$ The derivatives $f_x$ and $f_y$ are zero only at $(0,0)$. Applying the second derivative test there: $$D(0,0)=f_{xx}(0,0)f_{yy}(0,0)-f_{xy}(0,0)^2= 2\cdot2-0=4>0$$ and $$f_{xx}(0,0)=2>0,$$ so there is a local minimum at $(0,0)$, and there are no other possibilities. $\square$
Example 14.7.3 Find all local maxima and minima for $f(x,y)=x^2-y^2$.
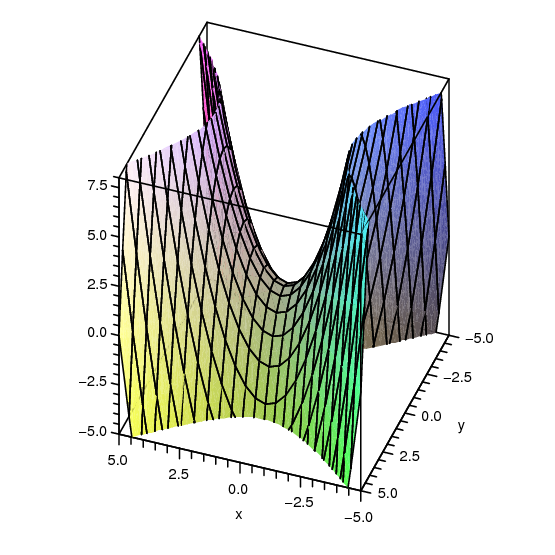
The derivatives: $$f_x=2x \qquad f_y=-2y \qquad f_{xx}=2 \qquad f_{yy}=-2 \qquad f_{xy}=0.$$ Again there is a single critical point, at $(0,0)$, and $$D(0,0)=f_{xx}(0,0)f_{yy}(0,0)-f_{xy}(0,0)^2= 2\cdot-2-0=-4< 0,$$ so there is neither a maximum nor minimum there, and so there are no local maxima or minima. The surface is shown in figure 14.7.1. $\square$
Example 14.7.4 Find all local maxima and minima for $f(x,y)=x^4+y^4$.
The derivatives: $$f_x=4x^3 \qquad f_y=4y^3 \qquad f_{xx}=12x^2 \qquad f_{yy}=12y^2 \qquad f_{xy}=0.$$ Again there is a single critical point, at $(0,0)$, and $$D(0,0)=f_{xx}(0,0)f_{yy}(0,0)-f_{xy}(0,0)^2= 0\cdot0-0=0,$$ so we get no information. However, in this case it is easy to see that there is a minimum at $(0,0)$, because $f(0,0)=0$ and at all other points $f(x,y)>0$. $\square$
Example 14.7.5 Find all local maxima and minima for $f(x,y)=x^3+y^3$.
The derivatives: $$f_x=3x^2 \qquad f_y=3y^2 \qquad f_{xx}=6x^2 \qquad f_{yy}=6y^2 \qquad f_{xy}=0.$$ Again there is a single critical point, at $(0,0)$, and $$D(0,0)=f_{xx}(0,0)f_{yy}(0,0)-f_{xy}(0,0)^2= 0\cdot0-0=0,$$ so we get no information. In this case, a little thought shows there is neither a maximum nor a minimum at $(0,0)$: when $x$ and $y$ are both positive, $f(x,y)>0$, and when $x$ and $y$ are both negative, $f(x,y)< 0$, and there are points of both kinds arbitrarily close to $(0,0)$. Alternately, if we look at the cross-section when $y=0$, we get $f(x,0)=x^3$, which does not have either a maximum or minimum at $x=0$. $\square$
Example 14.7.6 Suppose a box with no top is to hold a certain volume $V$. Find the dimensions for the box that result in the minimum surface area.
The area of the box is $A=2hw+2hl+lw$, and the volume is $V=lwh$, so we can write the area as a function of two variables, $$A(l,w)={2V\over l}+{2V\over w}+lw.$$ Then $$A_l=-{2V\over l^2}+w \quad\hbox{and}\quad A_w=-{2V\over w^2}+l.$$ If we set these equal to zero and solve, we find $\ds w=(2V)^{1/3}$ and $\ds l=(2V)^{1/3}$, and the corresponding height is $h=V/(2V)^{2/3}$.
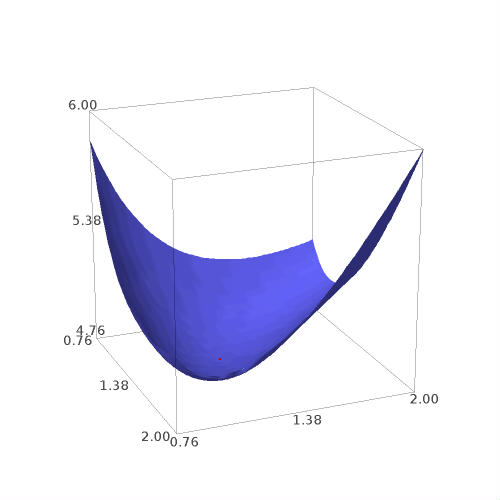
The second derivatives are $$A_{ll}={4V\over l^3}\qquad A_{ww}={4V\over w^3}\qquad A_{lw}=1,$$ so the discriminant is $$D={4V\over l^3}{4V\over w^3}-1=4-1=3>0.$$ Since $A_{ll}$ is 2, there is a local minimum at the critical point. Is this a global minimum? It is, but it is difficult to see this analytically; physically and graphically it is clear that there is a minimum, in which case it must be at the single critical point. Here is a portion of the graph with the minimum point shown.
Note that we must choose a value for $V$ in order to graph it. $\square$
Recall that when we did single variable global maximum and minimum problems, the easiest cases were those for which the variable could be limited to a finite closed interval, for then we simply had to check all critical values and the endpoints. The previous example is difficult because there is no finite boundary to the domain of the problem—both $w$ and $l$ can be in $(0,\infty)$. As in the single variable case, the problem is often simpler when there is a finite boundary.
Theorem 14.7.7 If $f(x,y)$ is continuous on a closed and bounded subset of $\R^2$, then it has both a maximum and minimum value. $\qed$
As in the case of single variable functions, this means that the maximum and minimum values must occur at a critical point or on the boundary; in the two variable case, however, the boundary is a curve, not merely two endpoints.
Example 14.7.8 The length of the diagonal of a box is to be 1 meter; find the maximum possible volume.
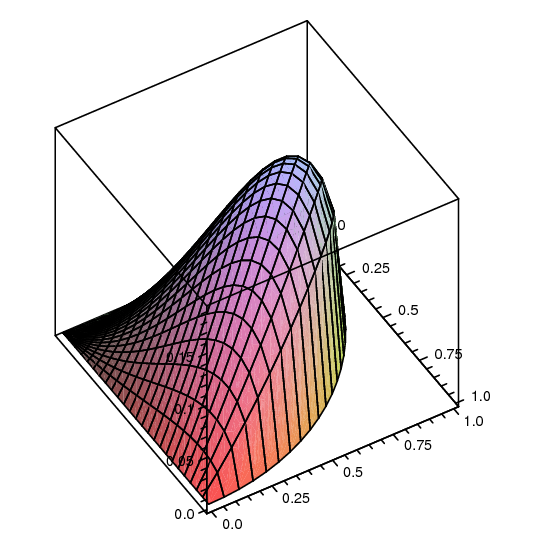
If the box is placed with one corner at the origin, and sides along the axes, the length of the diagonal is $\ds\sqrt{x^2+y^2+z^2}$, and the volume is $$V=xyz=xy\sqrt{1-x^2-y^2}.$$ Clearly, $x^2+y^2\le 1$, so the domain we are interested in is the quarter of the unit disk in the first quadrant. Computing derivatives: $$\eqalign{ V_x&={y-2yx^2-y^3\over\sqrt{1-x^2-y^2}}\cr V_y&={x-2xy^2-x^3\over\sqrt{1-x^2-y^2}}\cr }$$ If these are both 0, then $x=0$ or $y=0$, or $x=y=1/\sqrt3$. The boundary of the domain is composed of three curves: $x=0$ for $y\in[0,1]$; $y=0$ for $x\in[0,1]$; and $x^2+y^2=1$, where $x\ge0$ and $y\ge0$. In all three cases, the volume $xy\sqrt{1-x^2-y^2}$ is 0, so the maximum occurs at the only critical point $(1/\sqrt3,1/\sqrt3,1/\sqrt3)$, giving a volume of $1/(3\sqrt{3})$. See figure 14.7.2. $\square$
Exercises 14.7
Sage can do much of the work required to solve max/min problems. Shown is some work for example 14.7.8. Note that there are many solutions that make $f_x=0$ and $f_y=0$, but because of the nature of the problem, we know both $x$ and $y$ must be positive. In line 7 below, with a little tricky Sage code, we pick out the only solution with both $x$ and $y$ positive. After computing the solution, we can also use Sage to test whether it corresponds to a local maximum or local minimum.
Ex 14.7.1 Find all local maximum and minimum points of $f=x^2+4y^2-2x+8y-1$. (answer)
Ex 14.7.2 Find all local maximum and minimum points of $f=x^2-y^2+6x-10y+2$. (answer)
Ex 14.7.3 Find all local maximum and minimum points of $f=xy$. (answer)
Ex 14.7.4 Find all local maximum and minimum points of $f=9+4x-y-2x^2-3y^2$. (answer)
Ex 14.7.5 Find all local maximum and minimum points of $f=x^2+4xy+y^2-6y+1$. (answer)
Ex 14.7.6 Find all local maximum and minimum points of $f=x^2-xy+2y^2-5x+6y-9$. (answer)
Ex 14.7.7 Find the absolute maximum and minimum points of $f=x^2+3y-3xy$ over the region bounded by $y=x$, $y=0$, and $x=2$. (answer)
Ex 14.7.8 A six-sided rectangular box is to hold $1/2$ cubic meter; what shape should the box be to minimize surface area? (answer)
Ex 14.7.9 The post office will accept packages whose combined length and girth is at most 130 inches. (Girth is the maximum distance around the package perpendicular to the length; for a rectangular box, the length is the largest of the three dimensions.) What is the largest volume that can be sent in a rectangular box? (answer)
Ex 14.7.10 The bottom of a rectangular box costs twice as much per unit area as the sides and top. Find the shape for a given volume that will minimize cost. (answer)
Ex 14.7.11 Using the methods of this section, find the shortest distance from the origin to the plane $x+y+z=10$. (answer)
Ex 14.7.12 Using the methods of this section, find the shortest distance from the point $(x_0,y_0,z_0)$ to the plane $ax+by+cz=d$. You may assume that $c\not=0$; use of Sage or similar software is recommended. (answer)
Ex 14.7.13 A trough is to be formed by bending up two sides of a long metal rectangle so that the cross-section of the trough is an isosceles trapezoid, as in figure 6.2.6. If the width of the metal sheet is 2 meters, how should it be bent to maximize the volume of the trough? (answer)
Ex 14.7.14 Given the three points $(1,4)$, $(5,2)$, and $(3,-2)$, $\ds(x-1)^2+(y-4)^2+(x-5)^2+(y-2)^2+(x-3)^2+(y+2)^2$ is the sum of the squares of the distances from point $(x,y)$ to the three points. Find $x$ and $y$ so that this quantity is minimized. (answer)
Ex 14.7.15 Suppose that $f(x,y)=x^2+y^2+kxy$. Find and classify the critical points, and discuss how they change when $k$ takes on different values.
Ex 14.7.16 Find the shortest distance from the point $(0,b)$ to the parabola $y=x^2$. (answer)
Ex 14.7.17 Find the shortest distance from the point $(0,0,b)$ to the paraboloid $z=x^2+y^2$. (answer)
Ex 14.7.18 Consider the function $f(x,y)=x^3-3x^2y+y^3$.
a. Show that $(0,0)$ is the only critical point of $f$.
b. Show that the discriminant test is inconclusive for $f$.
c. Determine the cross-sections of $f$ obtained by setting $y=kx$ for various values of $k$.
d. What kind of critical point is $(0,0)$?
Ex 14.7.19 Find the volume of the largest rectangular box with edges parallel to the axes that can be inscribed in the ellipsoid $2x^2+72y^2+18z^2=288$. (answer)