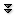As we have defined it in Section 1.3, a function is a very general object. At this point, it is useful to introduce a collection of properties of functions; knowing that a function has one of these properties can be very useful. Consider the graphs of the functions in Figure 2.5.1. It would clearly be useful to have words to help us describe the distinct features of each of them. We will point out and define a few properties (there are many more) of the functions pictured here. For the sake of the discussion, we will assume that the graphs do not exhibit any unusual behavior off-stage (i.e., outside the view of the graphs).
| (a) | (b) |
| (c) | (d) |
Functions. Each graph in Figure 2.5.1 certainly represents a function—since each passes the vertical line test. In other words, as you sweep a vertical line across the graph of each function, the line never intersects the graph more than once. If it did, then the graph would not represent a function.
Bounded. The graph in (c) appears to approach zero as $x$ goes to both positive and negative infinity. It also never exceeds the value $1$ or drops below the value $0$. Because the graph never increases or decreases without bound, we say that the function represented by the graph in (c) is a bounded function.
Definition 2.5.1 (Bounded) A function $f$ is bounded if there is a number $M$ such that $|f(x)| < M$ for every $x$ in the domain of $f$. $\square$
For the function in (c), one such choice for $M$ would be $10$. However, the smallest (optimal) choice would be $M=1$. In either case, simply finding an $M$ is enough to establish boundedness. No such $M$ exists for the hyperbola in (d) and hence we say that it is unbounded.
Continuity. The graphs shown in (b) and (c) both represent continuous functions. Geometrically, this is because there are no jumps in the graphs. That is, if you pick a point on the graph and approach it from the left and right, the values of the function approach the value of the function at that point. For example, we can see that this is not true for function values near $x=-1$ on the graph in (a) which is not continuous at that location.
Definition 2.5.2 (Continuous at a Point) A function $f$ is continuous at a point $a$ if $\ds \lim_{x\to a} f(x) = f(a)$. $\square$
Definition 2.5.3 (Continuous) A function $f$ is continuous if it is continuous at every point in its domain. $\square$
Strangely, we also say that (d) is continuous even though there is a vertical asymptote. A careful reading of the definition of continuous reveals the phrase "at every point in its domain.'' Because the location of the asymptote, $x=0$, is not in the domain of the function, and because the rest of the function is continuous, we say that (d) is continuous.
Differentiability. If a function has a derivative at every point, we say the function is differentiable. We can see that the tangent line is well-defined at every point on the graph in (c). Therefore, we say that (c) is a differentiable function.
Definition 2.5.4 (Differentiable at a Point) A function $f$ is differentiable at point $a$ if $f'(a)$ exists. $\square$
Definition 2.5.5 (Differentiable) A function $f$ is differentiable if is differentiable at every point (excluding endpoints and isolated points in the domain of $f$) in the domain of $f$. $\square$
Take note that, for technical reasons not discussed here, both of these definitions exclude endpoints and isolated points in the domain from consideration.
We close with a useful theorem about continuous functions:
Theorem 2.5.6 (Intermediate Value Theorem) If $f$ is continuous on the interval $[a,b]$ and $d$ is between $f(a)$ and $f(b)$, then there is a number $c$ in $[a,b]$ such that $f(c)=d$. $\qed$
This is most frequently used when $d=0$.
Example 2.5.7 Explain why the function $\ds f=x^3 + 3x^2+x-2$ has a root between 0 and 1.
By theorem 2.3.6, $f$ is continuous. Since $f(0)=-2$ and $f(1)=3$, and $0$ is between $-2$ and $3$, there is a $c\in[0,1]$ such that $f(c)=0$. $\square$
This example also points the way to a simple method for approximating roots.
Example 2.5.8 Approximate the root of the previous example to one decimal place.
If we compute $f(0.1)$, $f(0.2)$, and so on, we find that $f(0.6)< 0$ and $f(0.7)>0$, so by the Intermediate Value Theorem, $f$ has a root between $0.6$ and $0.7$. Repeating the process with $f(0.61)$, $f(0.62)$, and so on, we find that $f(0.61)< 0$ and $f(0.62)>0$, so $f$ has a root between $0.61$ and $0.62$, and the root is $0.6$ rounded to one decimal place. $\square$
Exercises 2.5
Ex 2.5.1 Along the lines of Figure 2.5.1, for each part below sketch the graph of a function that is:
a. bounded, but not continuous.
b. differentiable and unbounded.
c. continuous at $x=0$, not continuous at $x=1$, and bounded.
d. differentiable everywhere except at $x=-1$, continuous, and unbounded.
Ex 2.5.2 Is $f(x)=\sin(x)$ a bounded function? If so, find the smallest $M$. (answer)
Ex 2.5.3 Is $\ds s(t) = 1/(1+t^2)$ a bounded function? If so, find the smallest $M$. (answer)
Ex 2.5.4 Is $v(u) = 2\ln|u|$ a bounded function? If so, find the smallest $M$. (answer)
Ex 2.5.5 Consider the function $$h(x) = \cases{ 2x - 3, & if $x< 1$\cr 0, & if $x\geq 1$.}$$ Show that it is continuous at the point $x=0$. Is $h$ a continuous function? (answer)
Ex 2.5.6 Approximate a root of $\ds f=x^3-4x^2+2x+2$ to one decimal place. (answer)
Ex 2.5.7 Approximate a root of $\ds f=x^4+x^3-5x+1$ to one decimal place. (answer)