It will come as no surprise that we can also do triple integrals—integrals over a three-dimensional region. The simplest application allows us to compute volumes in an alternate way.
To approximate a volume in three dimensions, we can divide the three-dimensional region into small rectangular boxes, each $\Delta x\times\Delta y\times\Delta z$ with volume $\Delta x\Delta y\Delta z$. Then we add them all up and take the limit, to get an integral: $$\int_{x_0}^{x_1}\int_{y_0}^{y_1}\int_{z_0}^{z_1} dz\,dy\,dx.$$ If the limits are constant, we are simply computing the volume of a rectangular box.
Example 15.5.1 We use an integral to compute the volume of the box with opposite corners at $(0,0,0)$ and $(1,2,3)$. $$\int_0^1\int_0^2\int_0^3 dz\,dy\,dx=\int_0^1\int_0^2\left.z\right|_0^3 \,dy\,dx =\int_0^1\int_0^2 3\,dy\,dx =\int_0^1 \left.3y\right|_0^2 \,dx =\int_0^1 6\,dx = 6. $$ $\square$
Of course, this is more interesting and useful when the limits are not constant.
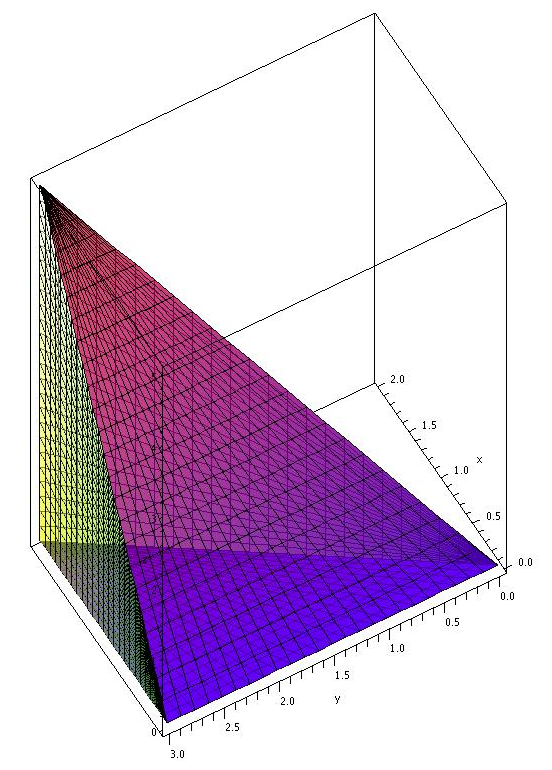
Example 15.5.2 Find the volume of the tetrahedron with corners at $(0,0,0)$, $(0,3,0)$, $(2,3,0)$, and $(2,3,5)$.
The whole problem comes down to correctly describing the region by inequalities: $0\le x\le 2$, $3x/2\le y\le 3$, $0\le z\le 5x/2$. The lower $y$ limit comes from the equation of the line $y=3x/2$ that forms one edge of the tetrahedron in the $x$-$y$ plane; the upper $z$ limit comes from the equation of the plane $z=5x/2$ that forms the "upper'' side of the tetrahedron; see figure 15.5.1. Now the volume is $$\eqalign{ \int_0^2\int_{3x/2}^3\int_0^{5x/2} dz\,dy\,dx &=\int_0^2\int_{3x/2}^3\left.z\right|_0^{5x/2} \,dy\,dx\cr &=\int_0^2\int_{3x/2}^3 {5x\over2}\,dy\,dx\cr &=\int_0^2 \left.{5x\over2}y\right|_{3x/2}^3 \,dx\cr &=\int_0^2 {15x\over2}-{15x^2\over4}\,dx\cr &=\left. {15x^2\over4}-{15x^3\over12}\right|_0^2\cr &=15-10=5.\cr }$$ $\square$
Pretty much just the way we did for two dimensions we can use triple integration to compute mass, center of mass, and various average quantities.
Example 15.5.3 Suppose the temperature at a point is given by $T=xyz$. Find the average temperature in the cube with opposite corners at $(0,0,0)$ and $(2,2,2)$.
In two dimensions we add up the temperature at "each'' point and divide by the area; here we add up the temperatures and divide by the volume, $8$: $$\eqalign{ {1\over8}\int_{0}^2\int_{0}^2\int_{0}^2 xyz\,dz\,dy\,dx &={1\over8}\int_{0}^2\int_{0}^2\left.{xyz^2\over2}\right|_0^2\,dy\,dx ={1\over16}\int_{0}^2\int_{0}^2 xy\,dy\,dx\cr &={1\over4}\int_{0}^2\left.{xy^2\over2}\right|_0^2\,dx ={1\over8}\int_{0}^2 4x\,dx ={1\over2}\left.{x^2\over2}\right|_0^2 =1.\cr }$$ $\square$
Example 15.5.4 Suppose the density of an object is given by $xz$, and the object occupies the tetrahedron with corners $(0,0,0)$, $(0,1,0)$, $(1,1,0)$, and $(0,1,1)$. Find the mass and center of mass of the object.
As usual, the mass is the integral of density over the region: $$\eqalign{ M&=\int_{0}^1\int_{x}^1\int_{0}^{y-x} xz\,dz\,dy\,dx =\int_{0}^1\int_{x}^1 {x(y-x)^2\over2}\,dy\,dx ={1\over2}\int_{0}^1 {x(1-x)^3\over3}\,dx\cr &={1\over6}\int_{0}^1 x-3x^2+3x^3-x^4\,dx ={1\over120}.\cr }$$ We compute moments as before, except now there is a third moment: $$\eqalign{ M_{xy} &= \int_{0}^1\int_{x}^1\int_{0}^{y-x} xz^2\,dz\,dy\,dx ={1\over360},\cr M_{xz} &= \int_{0}^1\int_{x}^1\int_{0}^{y-x} xyz\,dz\,dy\,dx ={1\over144},\cr M_{yz} &= \int_{0}^1\int_{x}^1\int_{0}^{y-x} x^2z\,dz\,dy\,dx ={1\over360}.\cr }$$ Finally, the coordinates of the center of mass are $\bar x=M_{yz}/M=1/3$, $\bar y=M_{xz}/M=5/6$, and $\bar z=M_{xy}/M=1/3$. $\square$
Exercises 15.5
Triple integrals in Sage are just like double integrals with, of course, an extra integral.
Ex 15.5.1 Evaluate $\ds\int_{0}^{1}\int_{0}^{x}\int_{0}^{x+y} 2x+y-1 \,dz\,dy\,dx$. (answer)
Ex 15.5.2 Evaluate $\ds\int_{0}^{2}\int_{-1}^{x^2}\int_{1}^{y} xyz \,dz\,dy\,dx$. (answer)
Ex 15.5.3 Evaluate $\ds\int_{0}^{1}\int_{0}^{x}\int_{0}^{\ln y} e^{x+y+z}\,dz\,dy\,dx$. (answer)
Ex 15.5.4 Evaluate $\ds\int_{0}^{\pi/2}\int_{0}^{\sin\theta}\int_{0}^{r\cos\theta} r^2\,dz\,dr\,d\theta$. (answer)
Ex 15.5.5 Evaluate $\ds\int_{0}^{\pi}\int_{0}^{\sin\theta}\int_{0}^{r\sin\theta} r\cos^2\theta\,dz\,dr\,d\theta$. (answer)
Ex 15.5.6 Evaluate $\ds\int_{0}^{1}\int_{0}^{y^2}\int_{0}^{x+y} x\,dz\,dx\,dy$. (answer)
Ex 15.5.7 Evaluate $\ds\int_{1}^{2}\int_{y}^{y^2}\int_{0}^{\ln(y+z)} e^x\,dx\,dz\,dy$. (answer)
Ex 15.5.8 Compute $\ds \int_0^\pi\int_0^{\pi/2}\int_0^1 z\sin x+z\cos y\,dz\,dy\,dx$. (answer)
Ex 15.5.9 For each of the integrals in the previous exercises, give a description of the volume (both algebraic and geometric) that is the domain of integration.
Ex 15.5.10 Compute $\ds\int\int\int x+y+z\,dV$ over the region $x^2+y^2+z^2\le 1$ in the first octant. (answer)
Ex 15.5.11 Find the mass of a cube with edge length 2 and density equal to the square of the distance from one corner. (answer)
Ex 15.5.12 Find the mass of a cube with edge length 2 and density equal to the square of the distance from one edge. (answer)
Ex 15.5.13 An object occupies the volume of the upper hemisphere of $x^2+y^2+z^2=4$ and has density $z$ at $(x,y,z)$. Find the center of mass. (answer)
Ex 15.5.14 An object occupies the volume of the pyramid with corners at $(1,1,0)$, $(1,-1,0)$, $(-1,-1,0)$, $(-1,1,0)$, and $(0,0,2)$ and has density $x^2+y^2$ at $(x,y,z)$. Find the center of mass. (answer)
Ex 15.5.15 Verify the moments $M_{xy}$, $M_{xz}$, and $M_{yz}$ of example 15.5.4 by evaluating the integrals.
Ex 15.5.16 Find the region $E$ for which $\ds\tint{E} (1-x^2-y^2-z^2) \; dV$ is a maximum.