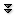We still have not answered one of our first questions about the steepness of a surface: starting at a point on a surface given by $f(x,y)$, and walking in a particular direction, how steep is the surface? We are now ready to answer the question.
We already know roughly what has to be done: as shown in figure 14.3.1, we extend a line in the $x$-$y$ plane to a vertical plane, and we then compute the slope of the curve that is the cross-section of the surface in that plane. The major stumbling block is that what appears in this plane to be the horizontal axis, namely the line in the $x$-$y$ plane, is not an actual axis—we know nothing about the "units'' along the axis. Our goal is to make this line into a $t$ axis; then we need formulas to write $x$ and $y$ in terms of this new variable $t$; then we can write $z$ in terms of $t$ since we know $z$ in terms of $x$ and $y$; and finally we can simply take the derivative.
So we need to somehow "mark off'' units on the line, and we need a convenient way to refer to the line in calculations. It turns out that we can accomplish both by using the vector form of a line. Suppose that ${\bf u}$ is a unit vector $\langle u_1,u_2\rangle$ in the direction of interest. A vector equation for the line through $(x_0,y_0)$ in this direction is ${\bf v}(t)=\langle u_1t+x_0,u_2t+y_0\rangle$. The height of the surface above the point $(u_1t+x_0,u_2t+y_0)$ is $g(t)=f(u_1t+x_0,u_2t+y_0)$. Because $\bf u$ is a unit vector, the value of $t$ is precisely the distance along the line from $(x_0,y_0)$ to $(u_1t+x_0,u_2t+y_0)$; this means that the line is effectively a $t$ axis, with origin at the point $(x_0,y_0)$, so the slope we seek is $$\eqalign{ g'(0)&=\langle f_x(x_0,y_0),f_y(x_0,y_0)\rangle\cdot \langle u_1,u_2\rangle\cr &=\langle f_x,f_y\rangle\cdot{\bf u}\cr &=\nabla f\cdot {\bf u}\cr }$$ Here we have used the chain rule and the derivatives ${d\over dt}(u_1t+x_0)=u_1$ and ${d\over dt}(u_2t+y_0)=u_2$. The vector $\langle f_x,f_y\rangle$ is very useful, so it has its own symbol, $\nabla f$, pronounced "del f''; it is also called the gradient of $f$.
Example 14.5.1 Find the slope of $z=x^2+y^2$ at $(1,2)$ in the direction of the vector $\langle 3,4\rangle$.
We first compute the gradient at $(1,2)$: $\nabla f=\langle 2x,2y\rangle$, which is $\langle 2,4\rangle$ at $(1,2)$. A unit vector in the desired direction is $\langle 3/5,4/5\rangle$, and the desired slope is then $\langle 2,4\rangle\cdot\langle 3/5,4/5\rangle=6/5+16/5=22/5$. $\square$
When doing such problems, it is easy to forget that we require a unit vector in the calculation $\nabla f\cdot {\bf u}$. You may prefer to remember that this can always be written as $\nabla f\cdot {\bf v}/|{\bf v}|$. In the previous example, we might then have computed $\langle 2,4\rangle\cdot\langle 3,4\rangle/|\langle 3,4\rangle|$, rather than remembering to first compute ${\bf u}=\langle 3,4\rangle/|\langle 3,4\rangle|$.
Example 14.5.2 Find a tangent vector to $z=x^2+y^2$ at $(1,2)$ in the direction of the vector $\langle 3,4\rangle$ and show that it is parallel to the tangent plane at that point.
Since $\langle 3/5,4/5\rangle$ is a unit vector in the desired direction, we can easily expand it to a tangent vector simply by adding the third coordinate computed in the previous example: $\langle 3/5,4/5,22/5\rangle$. To see that this vector is parallel to the tangent plane, we can compute its dot product with a normal to the plane. We know that a normal to the tangent plane is $$\langle f_x(1,2),f_y(1,2),-1\rangle = \langle 2,4,-1\rangle,$$ and the dot product is $\langle 2,4,-1\rangle\cdot\langle 3/5,4/5,22/5\rangle=6/5+16/5-22/5=0$, so the two vectors are perpendicular. (Note that the vector normal to the surface, namely $\langle f_x,f_y,-1\rangle$, is simply the gradient with a $-1$ tacked on as the third component.) $\square$
The slope of a surface given by $z=f(x,y)$ in the direction of a (two-dimensional) unit vector $\bf u$ is called the directional derivative of $f$, written $D_{\bf u}f$. The directional derivative immediately provides us with some additional information. We know that $$D_{\bf u}f=\nabla f\cdot {\bf u}=|\nabla f||{\bf u}|\cos\theta= |\nabla f|\cos\theta$$ if $\bf u$ is a unit vector; $\theta$ is the angle between $\nabla f$ and $\bf u$. This tells us immediately that the largest value of $D_{\bf u}f$ occurs when $\cos\theta=1$, namely, when $\theta=0$, so $\nabla f$ is parallel to $\bf u$. In other words, the gradient $\nabla f$ points in the direction of steepest ascent of the surface, and $|\nabla f|$ is the slope in that direction. Likewise, the smallest value of $D_{\bf u}f$ occurs when $\cos\theta=-1$, namely, when $\theta=\pi$, so $\nabla f$ is anti-parallel to $\bf u$. In other words, $-\nabla f$ points in the direction of steepest descent of the surface, and $-|\nabla f|$ is the slope in that direction.
Example 14.5.3 Investigate the direction of steepest ascent and descent for $z=x^2+y^2$.
The gradient is $\langle 2x,2y\rangle=2\langle x,y\rangle$; this is a vector parallel to the vector $\langle x,y\rangle$, so the direction of steepest ascent is directly away from the origin, starting at the point $(x,y)$. The direction of steepest descent is thus directly toward the origin from $(x,y)$. Note that at $(0,0)$ the gradient vector is $\langle 0,0\rangle$, which has no direction, and it is clear from the plot of this surface that there is a minimum point at the origin, and tangent vectors in all directions are parallel to the $x$-$y$ plane. $\square$
If $\nabla f$ is perpendicular to $\bf u$, $D_{\bf u}f=|\nabla f|\cos(\pi/2)=0$, since $\cos(\pi/2)=0$. This means that in either of the two directions perpendicular to $\nabla f$, the slope of the surface is 0; this implies that a vector in either of these directions is tangent to the level curve at that point. Starting with $\nabla f=\langle f_x,f_y\rangle$, it is easy to find a vector perpendicular to it: either $\langle f_y,-f_x\rangle$ or $\langle -f_y,f_x\rangle$ will work.
If $f(x,y,z)$ is a function of three variables, all the calculations proceed in essentially the same way. The rate at which $f$ changes in a particular direction is $\nabla f\cdot{\bf u}$, where now $\nabla f=\langle f_x,f_y,f_z\rangle$ and ${\bf u}=\langle u_1,u_2,u_3\rangle$ is a unit vector. Again $\nabla f$ points in the direction of maximum rate of increase, $-\nabla f$ points in the direction of maximum rate of decrease, and any vector perpendicular to $\nabla f$ is tangent to the level surface $f(x,y,z)=k$ at the point in question. Of course there are no longer just two such vectors; the vectors perpendicular to $\nabla f$ describe the tangent plane to the level surface, or in other words $\nabla f$ is a normal to the tangent plane.
Example 14.5.4 Suppose the temperature at a point in space is given by $T(x,y,z)=T_0/(1+x^2+y^2+z^2)$; at the origin the temperature in Kelvin is $T_0>0$, and it decreases in every direction from there. It might be, for example, that there is a source of heat at the origin, and as we get farther from the source, the temperature decreases. The gradient is $$\eqalign{ \nabla T&=\langle {-2T_0x\over (1+x^2+y^2+z^2)^2}, {-2T_0y\over (1+x^2+y^2+z^2)^2},{-2T_0z\over (1+x^2+y^2+z^2)^2}\rangle\cr &={-2T_0\over (1+x^2+y^2+z^2)^2}\langle x,y,z\rangle.\cr }$$ The gradient points directly at the origin from the point $(x,y,z)$—by moving directly toward the heat source, we increase the temperature as quickly as possible. $\square$
Example 14.5.5 Find the points on the surface defined by $x^2+2y^2+3z^2=1$ where the tangent plane is parallel to the plane defined by $3x-y+3z=1$.
Two planes are parallel if their normals are parallel or anti-parallel, so we want to find the points on the surface with normal parallel or anti-parallel to $\langle 3,-1,3\rangle$. Let $f=x^2+2y^2+3z^2$; the gradient of $f$ is normal to the level surface at every point, so we are looking for a gradient parallel or anti-parallel to $\langle 3,-1,3\rangle$. The gradient is $\langle 2x,4y,6z\rangle$; if it is parallel or anti-parallel to $\langle 3,-1,3\rangle$, then $$\langle 2x,4y,6z\rangle=k\langle 3,-1,3\rangle$$ for some $k$. This means we need a solution to the equations $$2x=3k\qquad 4y=-k\qquad 6z=3k$$ but this is three equations in four unknowns—we need another equation. What we haven't used so far is that the points we seek are on the surface $x^2+2y^2+3z^2=1$; this is the fourth equation. If we solve the first three equations for $x$, $y$, and $z$ and substitute into the fourth equation we get $$\eqalign{ 1&=\left({3k\over2}\right)^2+2\left({-k\over4}\right)^2+3\left({3k\over6}\right)^2\cr &=\left({9\over4}+{2\over16}+{3\over4}\right)k^2\cr &={25\over8}k^2\cr }$$ so $\ds k=\pm{2\sqrt2\over 5}$. The desired points are $\ds\left({3\sqrt2\over5},-{\sqrt2\over10},{\sqrt2\over 5}\right)$ and $\ds\left(-{3\sqrt2\over5},{\sqrt2\over10},-{\sqrt2\over 5}\right)$. The ellipsoid and the three planes are shown in figure 14.5.1.
Exercises 14.5
It's easy to compute directional derivatives in Sage.
Ex 14.5.1 Find $D_{\bf u} f$ for $\ds f=x^2+xy+y^2$ in the direction of ${\bf v}=\langle 2,1\rangle$ at the point $(1,1)$. (answer)
Ex 14.5.2 Find $D_{\bf u} f$ for $\ds f=\sin(xy)$ in the direction of ${\bf v}=\langle -1,1\rangle$ at the point $(3,1)$. (answer)
Ex 14.5.3 Find $D_{\bf u} f$ for $\ds f=e^x\cos(y)$ in the direction 30 degrees from the positive $x$ axis at the point $(1,\pi/4)$. (answer)
Ex 14.5.4 The temperature of a thin plate in the $x$-$y$ plane is $\ds T=x^2+y^2$. How fast does temperature change at the point $(1,5)$ moving in a direction 30 degrees from the positive $x$ axis? (answer)
Ex 14.5.5 Suppose the density of a thin plate at $(x,y)$ is $\ds 1/\sqrt{x^2+y^2+1}$. Find the rate of change of the density at $(2,1)$ in a direction $\pi/3$ radians from the positive $x$ axis. (answer)
Ex 14.5.6 Suppose the electric potential at $(x,y)$ is $\ds\ln\sqrt{x^2+y^2}$. Find the rate of change of the potential at $(3,4)$ toward the origin and also in a direction at a right angle to the direction toward the origin. (answer)
Ex 14.5.7 A plane perpendicular to the $x$-$y$ plane contains the point $(2,1,8)$ on the paraboloid $z=x^2+4y^2$. The cross-section of the paraboloid created by this plane has slope 0 at this point. Find an equation of the plane. (answer)
Ex 14.5.8 A plane perpendicular to the $x$-$y$ plane contains the point $(3,2,2)$ on the paraboloid $36z=4x^2+9y^2$. The cross-section of the paraboloid created by this plane has slope 0 at this point. Find an equation of the plane. (answer)
Ex 14.5.9 Suppose the temperature at $(x,y,z)$ is given by $\ds T=xy+\sin(yz)$. In what direction should you go from the point $(1,1,1)$ to decrease the temperature as quickly as possible? What is the rate of change of temperature in this direction? (answer)
Ex 14.5.10 Suppose the temperature at $(x,y,z)$ is given by $\ds T=xyz$. In what direction can you go from the point $(1,1,1)$ to maintain the same temperature? (answer)
Ex 14.5.11 Find an equation for the plane tangent to $\ds x^2-3y^2+z^2=7$ at $(1,1,3)$. (answer)
Ex 14.5.12 Find an equation for the plane tangent to $\ds xyz=6$ at $(1,2,3)$. (answer)
Ex 14.5.13 Find a vector function for the line normal to $\ds x^2+2y^2+4z^2=26 $ at $(2,-3,-1)$. (answer)
Ex 14.5.14 Find a vector function for the line normal to $\ds x^2+y^2+9z^2=56$ at $(4,2,-2)$. (answer)
Ex 14.5.15 Find a vector function for the line normal to $\ds x^2+5y^2-z^2=0$ at $(4,2,6)$. (answer)
Ex 14.5.16 Find the directions in which the directional derivative of $f(x,y)=x^2+\sin(xy)$ at the point $(1,0)$ has the value 1. (answer)
Ex 14.5.17 Show that the curve ${\bf r}(t) = \langle\ln(t),t\ln(t),t\rangle$ is tangent to the surface $xz^2-yz+\cos(xy) = 1$ at the point $(0,0,1)$.
Ex 14.5.18 A bug is crawling on the surface of a hot plate, the temperature of which at the point $x$ units to the right of the lower left corner and $y$ units up from the lower left corner is given by $T(x,y)=100-x^2-3y^3$.
a. If the bug is at the point $(2,1)$, in what direction should it move to cool off the fastest? How fast will the temperature drop in this direction?
b. If the bug is at the point $(1,3)$, in what direction should it move in order to maintain its temperature?
(answer)
Ex 14.5.19 The elevation on a portion of a hill is given by $f(x,y) = 100 -4x^2 - 2y$. From the location above $(2,1)$, in which direction will water run? (answer)
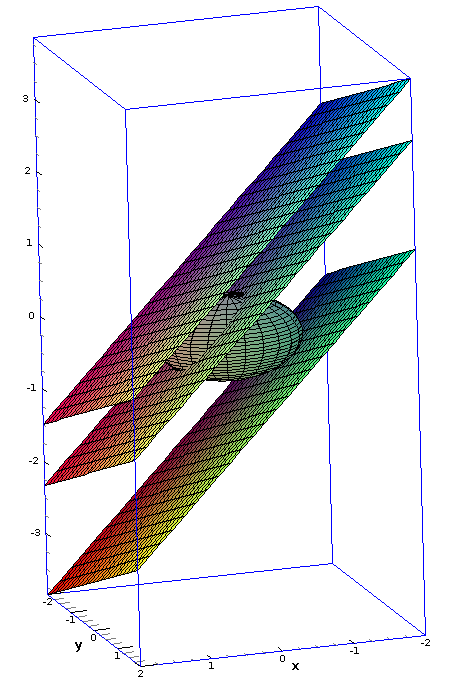
Ex 14.5.20 The contour map here shows wind speed in knots during Hurricane Andrew on August 24, 1992. Use it to estimate the value of the directional derivative of the wind speed at Homestead, FL, in the direction of the eye of the hurricane. Explain the meaning of your answer to a lay person. (answer)
Ex 14.5.21 Suppose that $g(x,y)=y-x^2$. Find the gradient at the point $(-1, 3)$. Sketch the level curve to the graph of $g$ when $g(x,y)=2$, and plot both the tangent line and the gradient vector at the point $(-1,3)$. (Make your sketch large). What do you notice, geometrically? (answer)
Ex 14.5.22 The gradient $\nabla f$ is a vector valued function of two variables. Prove the following gradient rules. Assume $f(x,y)$ and $g(x,y)$ are differentiable functions.
a. $\nabla(fg)=f\nabla(g)+g\nabla(f)$
b. $\nabla(f/g)=(g\nabla f - f \nabla g)/g^2$
c. $\nabla((f(x,y))^n)=nf(x,y)^{n-1}\nabla f$