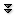What is the derivative of $\ds (x^2+1)/(x^3-3x)$? More generally, we'd like to have a formula to compute the derivative of $f(x)/g(x)$ if we already know $f'(x)$ and $g'(x)$. Instead of attacking this problem head-on, let's notice that we've already done part of the problem: $f(x)/g(x)= f(x)\cdot(1/g(x))$, that is, this is "really'' a product, and we can compute the derivative if we know $f'(x)$ and $(1/g(x))'$. So really the only new bit of information we need is $(1/g(x))'$ in terms of $g'(x)$. As with the product rule, let's set this up and see how far we can get: $$ \eqalign{ {d\over dx}{1\over g(x)}&=\lim_{\Delta x\to0} {{1\over g(x+\Delta x)}-{1\over g(x)}\over\Delta x}\cr &=\lim_{\Delta x\to0} {{g(x)-g(x+\Delta x)\over g(x+\Delta x)g(x)}\over\Delta x}\cr &=\lim_{\Delta x\to0} {g(x)-g(x+\Delta x)\over g(x+\Delta x)g(x)\Delta x}\cr &=\lim_{\Delta x\to0} -{g(x+\Delta x)-g(x)\over \Delta x} {1\over g(x+\Delta x)g(x)}\cr &=-{g'(x)\over g(x)^2}\cr }$$ Now we can put this together with the product rule: $${d\over dx}{f(x)\over g(x)}=f(x){-g'(x)\over g(x)^2}+f'(x){1\over g(x)}={-f(x)g'(x)+f'(x)g(x)\over g(x)^2}= {f'(x)g(x)-f(x)g'(x)\over g(x)^2}. $$
Example 3.4.1 Compute the derivative of $\ds (x^2+1)/(x^3-3x)$. $${d\over dx}{x^2+1\over x^3-3x}={2x(x^3-3x)-(x^2+1)(3x^2-3)\over(x^3-3x)^2}= {-x^4-6x^2+3\over (x^3-3x)^2}. $$
$\square$
It is often possible to calculate derivatives in more than one way, as we have already seen. Since every quotient can be written as a product, it is always possible to use the product rule to compute the derivative, though it is not always simpler.
Example 3.4.2 Find the derivative of $\ds \sqrt{625-x^2}/\sqrt{x}$ in two ways: using the quotient rule, and using the product rule.
Quotient rule: $${d\over dx}{\sqrt{625-x^2}\over\sqrt{x}} = {\sqrt{x}(-x/\sqrt{625-x^2})-\sqrt{625-x^2}\cdot 1/(2\sqrt{x})\over x}.$$ Note that we have used $\ds \sqrt{x}=x^{1/2}$ to compute the derivative of $\ds \sqrt{x}$ by the power rule.
Product rule: $${d\over dx}\sqrt{625-x^2} x^{-1/2} = \sqrt{625-x^2} {-1\over 2}x^{-3/2}+{-x\over \sqrt{625-x^2}}x^{-1/2}. $$
With a bit of algebra, both of these simplify to $$-{x^2+625\over 2\sqrt{625-x^2}x^{3/2}}.$$
$\square$
Occasionally you will need to compute the derivative of a quotient with a constant numerator, like $\ds 10/x^2$. Of course you can use the quotient rule, but it is usually not the easiest method. If we do use it here, we get $${d\over dx}{10\over x^2}={x^2\cdot 0-10\cdot 2x\over x^4}= {-20\over x^3},$$ since the derivative of 10 is 0. But it is simpler to do this: $${d\over dx}{10\over x^2}={d\over dx}10x^{-2}=-20x^{-3}.$$ Admittedly, $\ds x^2$ is a particularly simple denominator, but we will see that a similar calculation is usually possible. Another approach is to remember that $${d\over dx}{1\over g(x)}={-g'(x)\over g(x)^2},$$ but this requires extra memorization. Using this formula, $${d\over dx}{10\over x^2}=10{-2x\over x^4}.$$ Note that we first use linearity of the derivative to pull the 10 out in front.
Exercises 3.4
Find the derivatives of the functions in 1–4 using the quotient rule.
Ex 3.4.1 $\ds {x^3\over x^3-5x+10}$ (answer)
Ex 3.4.2 $\ds {x^2+5x-3\over x^5-6x^3+3x^2-7x+1}$ (answer)
Ex 3.4.3 $\ds {\sqrt{x}\over\sqrt{625-x^2}}$ (answer)
Ex 3.4.4 $\ds {\sqrt{625-x^2}\over x^{20}}$ (answer)
Ex 3.4.5 Find an equation for the tangent line to $\ds f(x) = (x^2 - 4)/(5-x)$ at $x= 3$. (answer)
Ex 3.4.6 Find an equation for the tangent line to $\ds f(x) = (x-2)/(x^3 + 4x - 1)$ at $x=1$. (answer)
Ex 3.4.7 Let $P$ be a polynomial of degree $n$ and let $Q$ be a polynomial of degree $m$ (with $Q$ not the zero polynomial). Using sigma notation we can write $$P=\sum _{k=0 } ^n a_k x^k,\qquad Q=\sum_{k=0}^m b_k x^k. $$ Use sigma notation to write the derivative of the rational function $P/Q$.
Ex 3.4.8 The curve $\ds y=1/(1+x^2)$ is an example of a class of curves each of which is called a witch of Agnesi. Sketch the curve and find the tangent line to the curve at $x= 5$. (The word witch here is a mistranslation of the original Italian, as described at http://mathworld.wolfram.com/WitchofAgnesi.html and http://witchofagnesi.org/. (answer)
Ex 3.4.9 If $f'(4) = 5$, $g'(4) = 12$, $(fg)(4)= f(4)g(4)=2$, and $g(4) = 6$, compute $f(4)$ and $\ds{d\over dx}{f\over g}$ at 4. (answer)