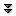Burnside's Theorem will allow us to count the orbits, that is, the different colorings, in a variety of problems. We first need some lemmas.
If $c$ is a coloring, $[c]$ is the orbit of $c$, that is, the equivalence class of $c$. Let $G(c)$ be the set of permutations in $G$ that fix $c$, that is, those $\phi$ such that $\phi(c)=c$; the permutation in figure 6.1.4 fixes the coloring in the bottom row, for example.
Lemma 6.2.1 $G(c)$ is a group of permutations.
Proof. We check the properties of a group from definition 6.1.1.
Suppose $\phi$ and $\sigma$ both fix $c$; then $\phi(\sigma(c))=\phi(c)=c$, so $\phi\circ\sigma$ fixes $c$ and $\phi\circ\sigma\in G(c)$.
The identity permutation fixes all colorings, so $\id\in G(c)$.
If $\phi(c)=c$ then $\phi^{-1}(c)=\phi^{-1}(\phi(c))=\id(c)=c$, so $\phi^{-1}\in G(c)$. $\qed$
Lemma 6.2.2 $|G|=|[c]|\cdot|G(c)|$.
Proof. For $\phi$ and $\sigma$ in $G$, define $\phi\sim\sigma$ if $\sigma^{-1}\circ\phi\in G(c)$. This is an equivalence relation:
1. $\sigma^{-1}\circ\sigma$ is the identity function, which is in $G(c)$. Thus $\sigma\sim\sigma$, so the relation is reflexive.
2. If $\phi\sim\sigma$, $\sigma^{-1}\circ\phi\in G(c)$. Then $(\sigma^{-1}\circ\phi)^{-1}\in G(c)$, and $(\sigma^{-1}\circ\phi)^{-1}=\phi^{-1}\circ\sigma\in G(c)$, so $\sigma\sim\phi$ and $\sim$ is symmetric.
3. If $\phi\sim\sigma$ and $\sigma\sim\tau$, then $\sigma^{-1}\circ\phi\in G(c)$ and $\tau^{-1}\circ\sigma\in G(c)$, so $(\tau^{-1}\circ\sigma)\circ(\sigma^{-1}\circ\phi)\in G(c)$. Since $(\tau^{-1}\circ\sigma)\circ(\sigma^{-1}\circ\phi)= \tau^{-1}\circ\phi$, $\phi\sim\tau$, and $\sim$ is transitive.
Now we claim that the equivalence class of $\phi$ is $A=\{\phi\circ\sigma\mid\sigma\in G(c)\}$. First, suppose that $\sigma\in G(c)$; then $\phi^{-1}\circ\phi\circ\sigma=\sigma\in G(c)$, so $\phi\circ\sigma\sim\phi$ and $A\subseteq[\phi]$. Next, suppose $\phi\sim\tau$, so $\tau^{-1}\circ\phi=\gamma\in G(c)$. Then $\phi\circ\gamma^{-1}=\tau$, so $\tau\in A$ and $[\phi]\subseteq A$.
Now we show that each equivalence class is the same size as $G(c)$. Define $f\colon G(c)\to \{\phi\circ\sigma\mid\sigma\in G(c)\}$ by $f(\gamma)=\phi\circ\gamma$. If $f(\gamma_1)=f(\gamma_2)$, then $$\eqalign{ \phi\circ\gamma_1&=\phi\circ\gamma_2\cr \phi^{-1}\circ\phi\circ\gamma_1&=\phi^{-1}\circ\phi\circ\gamma_2\cr \gamma_1&=\gamma_2\cr }$$ so $f$ is 1–1. Since every $\phi\circ\gamma\in\{\phi\circ\sigma\mid\sigma\in G(c)\}$ is $f(\gamma)$, $f$ is onto.
Thus the number of equivalence classes is $|G|/|G(c)|$.
Finally, we show that the number of equivalence classes is $|[c]|$. Let the set of equivalence classes in $G$ be $E$, that is, $E=\{[\phi]\mid \phi\in G\}$. We define $g\colon [c]\to E$ and show that $g$ is a bijection. Suppose $d\in[c]$, so $d=\sigma(c)$ for some $\sigma\in G$. Let $g(d)=[\sigma]$.
First, we show $g$ is well-defined. If $d=\sigma_1(c)=\sigma_2(c)$, then $\sigma_2^{-1}\circ\sigma_1(c)=c$, so $\sigma_1\sim\sigma_2$ and $[\sigma_1]=[\sigma_2]$, that is, $g(\sigma_1(c))=g(\sigma_2(c))$.
Next, suppose $g(d_1)=g(d_2)$. This means that $d_1=\sigma_1(c)$, $d_2=\sigma_2(c)$, and $[\sigma_1]=[\sigma_2]$. Hence $\sigma_2^{-1}\circ\sigma_1(c)=c$, so $\sigma_1(c)=\sigma_2(c)$ and thus $d_1=d_2$, so $g$ is 1–1.
Suppose that $[\sigma]\in E$. Then $g(\sigma(c))=[\sigma]$, so $g$ is onto.
Thus we have $$|[c]|=|E|={|G|\over|G(c)|}$$ and $$|G(c)|\cdot|[c]|=|G|$$ as desired. $\qed$
Corollary 6.2.3 If $c\sim d$ then $|G(c)|=|G(d)|$.
Proof. Since $c\sim d$, $[c]=[d]$, and $$\eqalign{ {|G|\over|G(c)|} = |[c]|&=|[d]|= {|G|\over|G(d)|}\cr |G(c)|&=|G(d)|\cr }$$ $\qed$
Definition 6.2.4 If group $G$ acts on the colorings of an object and $\sigma\in G$, $\fix(\sigma)$ is the set of colorings that are fixed by $\sigma$. $\square$
Theorem 6.2.5 (Burnside's Theorem) If group $G$ acts on the colorings of an object, the number of distinct colorings modulo $G$ is $${1\over|G|}\sum_{\sigma\in G} |\fix(\sigma)|.$$
Proof. Let $C$ be the set of all colorings, and let $\cal O$ be the set of orbits. Let $c_1,c_2,\ldots,c_k$ be a list of colorings, one in each orbit, so that the orbits are $[c_1],[c_2],\ldots,[c_k]$. Consider the sum $\ds\sum_{c\in C}|G(c)|$: $$\eqalign{ \sum_{c\in C}|G(c)|&=\sum_{i=1}^k\sum_{c\in[c_i]}|G(c)|\cr &=\sum_{i=1}^k\sum_{c\in[c_i]}|G(c_i)|\cr &=\sum_{i=1}^k\sum_{c\in[c_i]}{|G|\over|[c_i]|}\cr &=\sum_{i=1}^k |[c_i]|{|G|\over|[c_i]|}\cr &=\sum_{i=1}^k |G|=|G|\sum_{i=1}^k 1 = |G||{\cal O}|.\cr }$$ Then $$|{\cal O}| = {1\over|G|}\sum_{c\in C}|G(c)|.$$ This already gives an interesting formula for $|{\cal O}|$, but it is unwieldy, since the number of colorings is typically quite large; indeed, since we typically want to compute the number of orbits for $k$ colors, the number of colorings is not a fixed number.
With just a little more work we can fix this problem: $$\eqalign{ \sum_{c\in C}|G(c)|&=\sum_{c\in C}\sum_{\sigma\in G(c)} 1\cr &=\sum_{\sigma\in G}\sum_{c\in \fix(\sigma)} 1\cr &=\sum_{\sigma\in G}|\fix(\sigma)|.\cr }$$ Now $$|{\cal O}| = {1\over|G|}\sum_{\sigma\in G}|\fix(\sigma)|$$ as desired. $\qed$
Since the group of permutations in a typical problem is fairly small, the sum in Burnside's Theorem is usually manageable. Moreover, we can make the task of computing $|\fix(\sigma)|$ fairly straightforward. Let's consider a particular example, the permutation of figure 6.1.4, shown again in figure 6.2.1. If we are using $k$ colors, how many colorings of the pentagon are fixed by this permutation? Since the permutation swaps vertices 2 and 5, they must be the same color if $\phi$ is to fix the coloring. Likewise vertices 3 and 4 must be the same color; vertex 1 can be any color. Thus, the number of colorings fixed by $\phi$ is $k^3$. It is easy to see that every "flip'' permutation of the pentagon is essentially the same, so for each of the five flip permutations, the size of $\fix(\sigma)$ is $k^3$.
| $\phi\colon$ | $\longmapsto$ |
Every permutation can be written in cycle form: The permutation in figure 6.2.1, for example, is $(1)(2,5)(3,4)$. A cycle in this context is a sequence $(x_1,x_2,\ldots,x_k)$, meaning that $\phi(x_1)=x_2$, $\phi(x_2)=x_3$, and so on until $\phi(x_k)=x_1$. Following our reasoning above, the vertices in each cycle must be colored the same color, and the total number of colors fixed by $\phi$ is $k^m$, where $m$ is the number of cycles.
Let's apply this to another permutation, shown in figure 6.2.2. This permutation consists of a single cycle, so every vertex must have the same color, and the number of colorings fixed by $\phi$ is $k^1$. All rotations of the pentagon consist of a single cycle except the trivial rotation, that is, the identity permutation. In cycle form, the identity permutation is $(1)(2)(3)(4)(5)$, so the number of colorings fixed by the identity is $k^5$. Putting everything together, we thus have $$|{\cal O}|={1\over 10}(k^5+k+k+k+k+k^3+k^3+k^3+k^3+k^3)= {1\over 10}(k^5+5k^3+4k).$$ For example, the number of different 3-colorings is $(3^5+5\cdot3^3+4\cdot 3)/10=39$.
| $\phi\colon$ | $\longmapsto$ |
Example 6.2.6 We find the number of distinct colorings of the vertices of a square with $k$ colors, modulo $D_4$, the dihedral group of size 8. The elements of $D_4$ are the four rotations $r_0$, $r_{90}$, $r_{180}$, $r_{270}$, where $r_i$ is the counterclockwise rotation by $i$ degrees, and the four reflections $f_H$, $f_V$, $f_D$, $f_A$, as indicated in figure 6.2.3.
In cycle notation these permutations are: $$\eqalign{ r_0&=(1)(2)(3)(4)\cr r_{90}&=(1,4,3,2)\cr r_{180}&=(1,3)(2,4)\cr r_{270}&=(1,2,3,4)\cr f_H&=(1,4)(2,3)\cr f_V&=(1,2)(3,4)\cr f_D&=(1)(2,4)(3)\cr f_A&=(1,3)(2)(4).\cr }$$ so the number of colorings is $$f(k)={1\over 8}(k^4+k+k^2+k+k^2+k^2+k^3+k^3)={1\over8}(k^4+2k^3+3k^2+2k).$$ For example, $f(2)=6$; the six colorings are shown in figure 6.2.4. $\square$
Example 6.2.7 Here is a more complicated example: how many different graphs are there on four vertices? In this case, of course, "different'' means "non-isomorphic''. We can interpret this as a coloring problem: Color the edges of the complete graph $K_4$ with two colors, say black and white. The black edges form a graph; the white edges are the ones left out of the graph. The group $G$ we need to consider is all permutations of the six edges of $K_4$ induced by a permutation of the vertices, so $|G|=4!=24$. All we need to know is the number of cycles in each permutation; we consider a number of cases.
Case 1. The identity permutation on the vertices induces the identity permutation on the edges, with 6 cycles, so the contribution to the sum is $2^6$.
Case 2. A 4-cycle on the vertices induces a permutation of the edges consisting of one 4-cycle and one 2-cycle, that is, two cycles. There are $3!=6$ 4-cycles on the vertices, so the contribution of all of these is $6\cdot2^2$.
Case 3. A permutation of the vertices consisting of a 3-cycle and a 1-cycle induces a permutation of the edges consisting of two 3-cycles. There are $4\cdot2=8$ such permutations of the vertices, so the contribution of all is $8\cdot2^2$.
Case 4. A permutation of the vertices consisting of two 2-cycles induces a permutation of the edges consisting of two 1-cycles and two 2-cycles. There are ${1\over2}{4\choose2}=3$ such permutations, so the contribution is $3\cdot 2^4$.
Case 5. A permutation of the vertices consisting of a 2-cycle and two 1-cycles induces a permutation of the edges consisting of two 1-cycles and two 2-cycles. There are ${4\choose2}=6$ such permutations, so the contribution is $6\cdot 2^4$.
The number of distinct colorings, that is, the number of distinct graphs on four vertices, is $${1\over24}(2^6+6\cdot2^2+8\cdot2^2+3\cdot 2^4+6\cdot2^4)= {1\over24}(264)=11.$$ $\square$
It is possible, though a bit difficult, to see that for $n$ vertices the result is $$\eqalignno{ f(n)&=\sum_{\bf j}\prod_{k=1}^n{1\over k^{j_k} j_k!} \prod_{k=1}^{\lfloor n/2\rfloor}2^{k j_{2k}} \!\!\prod_{k=1}^{\lfloor (n-1)/2\rfloor}\!\!2^{kj_{2k+1}} \prod_{k=1}^{\lfloor n/2\rfloor} 2^{kC(j_k,2)} \!\!\!\!\prod_{1\le r< s\le n-1}\!\!\!\!\!\!\!\! 2^{\gcd(r,s)j_rj_s}\qquad (6.2.1)\cr} $$ where the sum is over all partitions ${\bf j}=(j_1,j_2,\ldots,j_n)$ of $n$, that is, over all $\bf j$ such that $j_1+2j_2+3j_3+\cdots+nj_n=n$, and $C(m,2)={m\choose2}$. With this formula and a computer it is easy to compute the number of graphs when $n$ is not too large; for example, $f(5)=34$, so there are 34 different five-vertex graphs.
In light of the forgoing discussion, we can restate theorem 6.2.5. If $\sigma$ is a permutation, let $\#\sigma$ denote the number of cycles when $\sigma$ is written in cycle form.
Corollary 6.2.8 If group $G$ acts on the colorings of an object, the number of distinct colorings modulo $G$ with $k$ colors is $${1\over|G|}\sum_{\sigma\in G} k^{\#\sigma}.$$ $\qed$
Exercises 6.2
Ex 6.2.1 Write the 12 permutations of the vertices of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron in cycle form. Use the labeling below.
Ex 6.2.2 Find the number of different colorings of the vertices of a regular tetrahedron with $k$ colors, modulo the rigid motions.
Ex 6.2.3 Write the 12 permutations of the edges of the regular tetrahedron corresponding to the 12 rigid motions of the regular tetrahedron in cycle form. Use the labeling below.
Ex 6.2.4 Find the number of different colorings of the edges of a regular tetrahedron with $k$ colors, modulo the rigid motions.
Ex 6.2.5 Find the number of non-isomorphic graphs on 5 vertices "by hand'', that is, using the method of example 6.2.7.