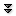Recall that $${n\choose k}={n!\over k!\,(n-k)!}={n(n-1)(n-2)\cdots(n-k+1)\over k!}.$$ The expression on the right makes sense even if $n$ is not a non-negative integer, so long as $k$ is a non-negative integer, and we therefore define $${r\choose k}={r(r-1)(r-2)\cdots(r-k+1)\over k!}$$ when $r$ is a real number. For example, $${1/2\choose 4}={(1/2)(-1/2)(-3/2)(-5/2)\over 4!}={-5\over128} \quad\hbox{and}\quad {-2\choose 3}={(-2)(-3)(-4)\over 3!}=-4. $$ These generalized binomial coefficients share some important properties of the usual binomial coefficients, most notably that $$\eqalignno{ {r\choose k}&={r-1\choose k-1}+{r-1\choose k}.& (3.1.1)\cr }$$ Then remarkably:
Theorem 3.1.1 (Newton's Binomial Theorem) For any real number $r$ that is not a non-negative integer, $$(x+1)^r=\sum_{i=0}^\infty {r\choose i}x^i$$ when $-1< x< 1$.
Proof. It is not hard to see that the series is the Maclaurin series for $(x+1)^r$, and that the series converges when $-1< x< 1$. It is rather more difficult to prove that the series is equal to $(x+1)^r$; the proof may be found in many introductory real analysis books. $\qed$
Example 3.1.2 Expand the function $(1-x)^{-n}$ when $n$ is a positive integer.
We first consider $(x+1)^{-n}$; we can simplify the binomial coefficients: $$\eqalign{ {(-n)(-n-1)(-n-2)\cdots(-n-i+1)\over i!} &=(-1)^i{(n)(n+1)\cdots(n+i-1)\over i!}\cr &=(-1)^i{(n+i-1)!\over i!\,(n-1)!}\cr &=(-1)^i{n+i-1\choose i}=(-1)^i{n+i-1\choose n-1}.\cr }$$ Thus $$(x+1)^{-n}=\sum_{i=0}^\infty (-1)^i{n+i-1\choose n-1}x^i =\sum_{i=0}^\infty {n+i-1\choose n-1}(-x)^i.$$ Now replacing $x$ by $-x$ gives $$(1-x)^{-n}=\sum_{i=0}^\infty {n+i-1\choose n-1}x^i.$$ So $(1-x)^{-n}$ is the generating function for ${n+i-1\choose n-1}$, the number of submultisets of $\{\infty\cdot1,\infty\cdot2,\ldots,\infty\cdot n\}$ of size $i$. $\square$
In many cases it is possible to directly construct the generating function whose coefficients solve a counting problem.
Example 3.1.3 Find the number of solutions to $\ds x_1+x_2+x_3+x_4=17$, where $0\le x_1\le2$, $0\le x_2\le5$, $0\le x_3\le5$, $2\le x_4\le6$.
We can of course solve this problem using the inclusion-exclusion formula, but we use generating functions. Consider the function $$(1+x+x^2)(1+x+x^2+x^3+x^4+x^5)(1+x+x^2+x^3+x^4+x^5)(x^2+x^3+x^4+x^5+x^6).$$ We can multiply this out by choosing one term from each factor in all possible ways. If we then collect like terms, the coefficient of $x^k$ will be the number of ways to choose one term from each factor so that the exponents of the terms add up to $k$. This is precisely the number of solutions to $\ds x_1+x_2+x_3+x_4=k$, where $0\le x_1\le2$, $0\le x_2\le5$, $0\le x_3\le5$, $2\le x_4\le6$. Thus, the answer to the problem is the coefficient of $x^{17}$. With the help of a computer algebra system we get $$\eqalign{ (1+x+x^2)(1&+x+x^2+x^3+x^4+x^5)^2(x^2+x^3+x^4+x^5+x^6)\cr =\;&x^{18} + 4x^{17} + 10x^{16} + 19x^{15} + 31x^{14} + 45x^{13} + 58x^{12} + 67x^{11} + 70x^{10}\cr &+67x^9 + 58x^8 + 45x^7 + 31x^6 + 19x^5 + 10x^4 + 4x^3 + x^2,\cr }$$ so the answer is 4. $\square$
Example 3.1.4 Find the generating function for the number of solutions to $\ds x_1+x_2+x_3+x_4=k$, where $0\le x_1\le\infty$, $0\le x_2\le5$, $0\le x_3\le5$, $2\le x_4\le6$.
This is just like the previous example except that $x_1$ is not bounded above. The generating function is thus $$\eqalign{ f(x)&=(1+x+x^2+\cdots)(1+x+x^2+x^3+x^4+x^5)^2(x^2+x^3+x^4+x^5+x^6)\cr &=(1-x)^{-1}(1+x+x^2+x^3+x^4+x^5)^2(x^2+x^3+x^4+x^5+x^6)\cr &={(1+x+x^2+x^3+x^4+x^5)^2(x^2+x^3+x^4+x^5+x^6)\over 1-x}. }$$ Note that $(1-x)^{-1}=(1+x+x^2+\cdots)$ is the familiar geometric series from calculus; alternately, we could use example 3.1.2. Unlike the function in the previous example, this function has an infinite expansion: $$\eqalign{ f(x)&= x^2+4x^3 + 10x^4 + 20x^5 +35x^6 + 55x^7+ 78x^8 \cr &+ 102x^9 + 125x^{10}+ 145x^{11} + 160x^{12} + 170x^{13}+176x^{14} \cr &+ 179x^{15} +180x^{16} + 180x^{17} + 180x^{18} + 180x^{19} + 180x^{20} +\cdots. }$$ Here is how to do this in Sage. $\square$
Example 3.1.5 Find a generating function for the number of submultisets of $\{\infty\cdot a,\infty\cdot b,\infty\cdot c\}$ in which there are an odd number of $a$s, an even number of $b$s, and any number of $c$s. As we have seen, this is the same as the number of solutions to $x_1+x_2+x_3=n$ in which $x_1$ is odd, $x_2$ is even, and $x_3$ is unrestricted. The generating function is therefore $$\eqalign{ (x+x^3+x^5&+\cdots)(1+x^2+x^4+\cdots)(1+x+x^2+x^3+\cdots)\cr &=x(1+(x^2)+(x^2)^2+(x^2)^3+\cdots)(1+(x^2)+(x^2)^2+(x^2)^3+\cdots){1\over 1-x}\cr &={x\over (1-x^2)^2(1-x)}.\cr }$$ $\square$
Exercises 3.1
For some of these exercises, you may want to use the sage applet above, in example 3.1.4, or your favorite computer algebra system.
Ex 3.1.1 Prove that ${r\choose k}={r-1\choose k-1}+{r-1\choose k}$.
Ex 3.1.2 Show that the Maclaurin series for $(x+1)^r$ is $\sum_{i=0}^\infty {r\choose i}x^i$.
Ex 3.1.3 Concerning example 3.1.4, show that all coefficients beginning with $x^{16}$ are 180.
Ex 3.1.4 Use a generating function to find the number of solutions to $\ds x_1+x_2+x_3+x_4=14$, where $0\le x_1\le3$, $2\le x_2\le5$, $0\le x_3\le5$, $4\le x_4\le6$.
Ex 3.1.5 Find the generating function for the number of solutions to $\ds x_1+x_2+x_3+x_4=k$, where $0\le x_1\le\infty$, $3\le x_2\le\infty$, $2\le x_3\le5$, $1\le x_4\le5$.
Ex 3.1.6 Find a generating function for the number of non-negative integer solutions to $3x+2y+7z=n$.
Ex 3.1.7 Suppose we have a large supply of red, white, and blue balloons. How many different bunches of 10 balloons are there, if each bunch must have at least one balloon of each color and the number of white balloons must be even?
Ex 3.1.8 Use generating functions to show that every positive integer can be written in exactly one way as a sum of distinct powers of 2.
Ex 3.1.9 Suppose we have a large supply of blue and green candles, and one gold candle. How many collections of $n$ candles are there in which the number of blue candles is even, the number of green candles is any number, and the number of gold candles is at most one?