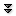Suppose we have a chess board, and a collection of tiles, like dominoes, each of which is the size of two squares on the chess board. Can the chess board be covered by the dominoes? First we need to be clear on the rules: the board is covered if the dominoes are laid down so that each covers exactly two squares of the board; no dominoes overlap; and every square is covered. The answer is easy: simply by laying out 32 dominoes in rows, the board can be covered. To make the problem more interesting, we allow the board to be rectangular of any size, and we allow some squares to be removed from the board. What can be say about whether the remaining board can be covered? This is such a board, for example:

What can we say? Here is an easy observation: each domino must cover two squares, so the total number of squares must be even; the board above has an even number of squares. Is that enough? It is not too hard to convince yourself that this board cannot be covered; is there some general principle at work? Suppose we redraw the board to emphasize that it really is part of a chess board:

Aha! Every tile must cover one white and one gray square, but there are four of the former and six of the latter, so it is impossible. Now do we have the whole picture? No; for example:

The gray square at the upper right clearly cannot be covered. Unfortunately it is not easy to state a condition that fully characterizes the boards that can be covered; we will see this problem again. Let us note, however, that this problem can also be represented as a graph problem. We introduce a vertex corresponding to each square, and connect two vertices by an edge if their associated squares can be covered by a single domino; here is the previous board:

Here the top row of vertices represents the gray squares, the bottom row the white squares. A domino now corresponds to an edge; a covering by dominoes corresponds to a collection of edges that share no endpoints and that are incident with (that is, touch) all six vertices. Since no edge is incident with the top left vertex, there is no cover.

Perhaps the most famous problem in graph theory concerns map coloring: Given a map of some countries, how many colors are required to color the map so that countries sharing a border get different colors? It was long conjectured that any map could be colored with four colors, and this was finally proved in 1976. Here is an example of a small map, colored with four colors:

Typically this problem is turned into a graph theory problem. Suppose we add to each country a capital, and connect capitals across common boundaries. Coloring the capitals so that no two connected capitals share a color is clearly the same problem. For the previous map:

Any graph produced in this way will have an important property: it can be drawn so that no edges cross each other; this is a planar graph. Non-planar graphs can require more than four colors, for example this graph:

This is called the complete graph on five vertices, denoted $K_5$; in a complete graph, each vertex is connected to each of the others. Here only the "fat'' dots represent vertices; intersections of edges at other points are not vertices. A few minutes spent trying should convince you that this graph cannot be drawn so that its edges don't cross, though the number of edge crossings can be reduced.

Exercises 1.1

Ex 1.1.1 Explain why an $m\times n$ board can be covered if either $m$ or $n$ is even. Explain why it cannot be covered if both $m$ and $n$ are odd.

Ex 1.1.2 Suppose two diagonally opposite corners of an ordinary $8\times8$ board are removed. Can the resulting board be covered?

Ex 1.1.3 Suppose that $m$ and $n$ are both odd. On an $m\times n$ board, colored as usual, all four corners will be the same color, say white. Suppose one white square is removed from any location on the board. Show that the resulting board can be covered.

Ex 1.1.4 Suppose that one corner of an $8\times8$ board is removed. Can the remainder be covered by $1\times 3$ tiles? Show a tiling or prove that it cannot be done.

Ex 1.1.5 Suppose the square in row 3, column 3 of an $8\times8$ board is removed. Can the remainder be covered by $1\times 3$ tiles? Show a tiling or prove that it cannot be done.

Ex 1.1.6 Remove two diagonally opposite corners of an $m\times n$ board, where $m$ is odd and $n$ is even. Show that the remainder can be covered with dominoes.

Ex 1.1.7 Suppose one white and one black square are removed from an $n\times n$ board, $n$ even. Show that the remainder can be covered by dominoes.

Ex 1.1.8 Suppose an $n\times n$ board, $n$ even, is covered with dominoes. Show that the number of horizontal dominoes with a white square under the left end is equal to the number of horizontal dominoes with a black square under the left end.

Ex 1.1.9 In the complete graph on five vertices shown above, there are five pairs of edges that cross. Draw this graph so that only one pair of edges cross. Remember that "edges'' do not have to be straight lines.

Ex 1.1.10 The complete bipartite graph $K_{3,3}$ consists of two groups of three vertices each, with all possible edges between the groups and no other edges:

Draw this graph with only one crossing.