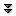We can interpret the sdr problem as a problem about graphs. Given sets $A_1,A_2,\ldots,A_n$, with $\bigcup_{i=1}^n A_i=\{x_1,x_2,\ldots,x_m\}$, we define a graph with $n+m$ vertices as follows: The vertices are labeled $\{A_1,A_2,\ldots,A_n,x_1,x_2,\ldots x_m\}$, and the edges are $\{\{A_i,x_j\}\mid x_j\in A_i\}$.
Example 4.4.1 Let $A_1=\{a,b,c,d\}$, $A_2=\{a,c,e,g\}$, $A_3=\{b,d\}$, and $A_4=\{a,f,g\}$. The corresponding graph is shown in figure 4.4.1. $\square$
Before exploring this idea, we introduce a few basic concepts about graphs. If two vertices in a graph are connected by an edge, we say the vertices are adjacent. If a vertex $v$ is an endpoint of edge $e$, we say they are incident. The set of vertices adjacent to $v$ is called the neighborhood of $v$, denoted $N(v)$. This is sometimes called the open neighborhood of $v$ to distinguish it from the closed neighborhood of $v$, $N[v]=N(v)\cup\{v\}$. The degree of a vertex $v$ is the number of edges incident with $v$; it is denoted $\d(v)$.
Some simple types of graph come up often: A path is a graph $P_n$ on vertices $v_1,v_2,\ldots,v_n$, with edges $\{v_i,v_{i+1}\}$ for $1\le i\le n-1$, and no other edges. A cycle is a graph $C_n$ on vertices $v_1,v_2,\ldots,v_n$ with edges $\{v_i,v_{1+(i\bmod n)}\}$ for $1\le i\le n$, and no other edges; this is a path in which the first and last vertices have been joined by an edge. (Generally, we require that a cycle have at least three vertices. If it has two, then the two are joined by two distinct edges; when a graph has more than one edge with the same endpoints it is called a multigraph. If a cycle has one vertex, there is an edge, called a loop, in which a single vertex serves as both endpoints.) The length of a path or cycle is the number of edges in the graph. For example, $P_1$ has length 0, $C_1$ has length 1. A complete graph $K_n$ is a graph on $v_1,v_2,\ldots,v_n$ in which every two distinct vertices are joined by an edge. See figure 4.4.2 for examples.
The graph in figure 4.4.1 is a bipartite graph.
Definition 4.4.2 A graph $G$ is bipartite if its vertices can be partitioned into two parts, say $\{v_1,v_2,\ldots,v_n\}$ and $\{w_1,w_2,\ldots,w_m\}$ so that all edges join some $v_i$ to some $w_j$; no two vertices $v_i$ and $v_j$ are adjacent, nor are any vertices $w_i$ and $w_j$. $\square$
The graph in figure 4.4.1 is bipartite, as are the first two graphs in figure 4.4.2.